Mean Kinetic Energy in Helium mixtures and nanoporous confinement

Collaborative research among scientists from Italy – the Nast Centre for Nanoscience Nanotechnology and Innovative Instrumentation, UK – ISIS Spallation Neutron Source – have studied the single particle microscopic dynamics of helium atoms (3He, 4He) in bulk and confined in silica nanopores, using Deep Inelastic Neutron Scattering (DINS) at the ISIS

Spallation neutron Source. The (DINS) technique provides direct information about single-particle dynamical properties, such as the momentum distribution, n(p), and the mean kinetic energy, <EK>.

Due to its light mass, its zero-point energy is large compared to thermal motions, Helium occupies a special role in condensed matter. The combination of the high zero-point energy with the weak inter-atomic forces gives to helium a unique property: it is the only element in nature with no liquid-solid transition at T=0 K (at atmospheric pressure). For this reason, quantum effects can be observed. On the other hand, other elements have strong interatomic forces or lower zero-point energies and usually their crystallization occurs at a freezing temperature well above that one at which quantum phenomena start to become significant. In the study of helium it is therefore of paramount importance to consider quantum effects, such as exchange effects and increasing of the mean kinetic energy due to the localization (Pauli principle). Moreover, condensed 4He, 3He and helium isotopic mixtures represent the simplest prototype examples of many-body systems, i.e. interacting bosons (4He) and fermions (3He).

Due to confinement or localization effects the <EK> value for helium in nanopores is expected to increase with respect to the value in bulk. In order to see this effect, one usually exploits two kinds of localization: a confinement obtained by adding 3He atoms to 4He, and a space confinement, using nanoporous systems.

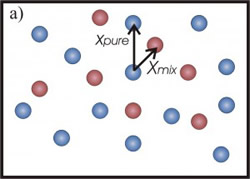mean-kinetic-energy _fig1a_sIn the first case (Fig.1-a), the 3He atoms border the 4He in a smaller space and the <EK> of the heavier isotope increases. A similar effect should be expected also for 3He mean kinetic energy. However, in this case it has been shown (C. Andreani, C. Pantalei, R. Senesi, “Mean kinetic energy of helium atoms in fluid 3He and 3He-4He mixtures”,Journal of Physics Condensed Matter (2007)) that the lighter isotope seems not to be affected by the presence of the 4He atoms and its kinetic energy seems to be independent of the mixture density. This behaviour can be explained by taking into account exchange effects: the 3He atoms interact with the same kind of isotope, feeling the effect of a density less than that one of isotopic mixture (fig.1-b).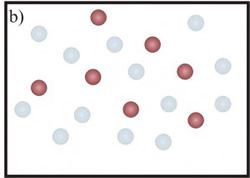mean-kinetic-energy _fig1b_s

Figure 1: a) Picture of 4He atoms (blue circles). With the addition of 3He atoms (red circles) the mean distance, among a helium atom and its neighbours, decreases (from xpure to xmix). The 4He atom is more localized and its mean kinetic energy increases. b) The 3He atoms is not affected by the presence of the 4He atoms (represented as transparent blue circles).

The other way to localize helium atoms is to confine them in porous powders with mean diameter of pores in a nanometric scale. Several efforts have been devoted to exploring the effect of this kind of confinement on the dynamics of 4He. Studies of adsorption of helium on a variety of surfaces have provided a wealth of information on the behaviour of low-dimensional quantum solids and their interaction with substrates.

The present study (C.Andreani, C. Pantalei, R. Senesi, ”4He adsorbed in cylindrical silica nanopores: size-effects on single atom mean kinetic energy”, Phys. Rev B, 75, 064515 (2007))had the aim of deriving the single-particle mean kinetic energy <EK> of 4He adsorbed in cylindrical silica nanopores (xerogel) for different pore diameters, namely, 24 Å and 160 Å. This study allowed to derive the dependence of single-particle dynamics on pore sizes, layer coverage, and geometry of the confining system.

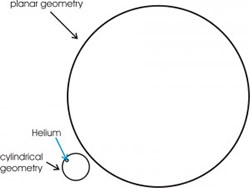
  • mean-kinetic-energy _fig2_s

    Figure 2: The picture represents, to scale, the two pores, with diameter of 24 Å and 160 Å. For the helium (blue circle) the smallest pore appears as a cylindrical geometry, the biggest one as a planar geometry.

    The choice of these two diameter was motivated by the interest to compare different kinds of geometry. In fact, to a good approximation, the corrugation experienced by helium atoms, close to a nanoporous surface, appears as a cylindrical surface, for the smallest one, and as a planar surface, for the biggest one (fig. 2).

    The single-particle dynamics of confined helium atoms is shown to be significantly affected by confinement and the <EK> values of helium adsorbed in xerogel powders are found significantly higher than those in bulk liquid. In particular, the mean kinetic energy increases by reducing the pore size. In this case, the behaviour of the kinetic energy is due to different reasons with respect to that explained in the case of the mixtures.

    mean-kinetic-energy _fig3_s

    Figure 3: The helium atoms (blue circles) arrange themselves in concentrical annuli, beginning with a first layer close to the surface. The number of atoms in each layer depends on the ratio between helium atom and pore diameters.

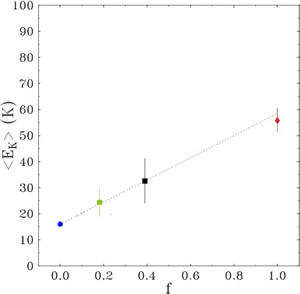
    In such nanoporous systems, a microscopic structural model assumes that the 4He atoms are arranged in concentric annuli along the cylindrical pore axis(Phys. Rev. B 72, 064516 (2005)), with the number of atoms in each layer depending on the ratio of the helium diameter to the pore diameter (fig. 3). The resulting mean kinetic-energy values are interpreted with a model of uncorrelated sum of contributions of two kinds of layers: liquid-like layers (giving a contribution in energy equal to the liquid bulk energy) and solid-like layers (with a higher energy contribution). In the case of 4He adsorbed in pores of 24 Å diameter, the experimental mean kinetic-energy value is well reproduced by assuming a single solid-like layer, with all other inner layers in the liquid phase. For the 4He adsorbed in pores of 160 Å diameter, the surface roughness plays a relevant role and the result is interpreted in terms of three solid-like layers. In fig 4 it is reported the mean kinetic energy as function of the fraction, f, between the number of atoms in the solid-like layers and the number of atoms in the liquid-like layers. The value of franges from f=0 (corresponding to the liquid bulk) to f=1 (corresponding to have only 1 solid-like layer), passing through the intermediate values, corresponding to a cylindrical and to a planar geometry.

    mean-kinetic-energy _fig4_s

    Fig. 4. Single-atom mean kinetic energies as a function of the ratio, f, between the number of atoms in solid and liquid layers. Blue circle: bulk liquid value. Squares: experimental value of <EK> for helium in xerogel powder (24 Å, black square; 160 Å, green square). Red diamond: experimental value of <EK> for helium adsorbed in active carbon fibers, (i.e., monolayer coverage, f=1, and slit geometry, (J. Phys.: Condens. Matter 11 No 35 (1999) ). The three experimental values for confined helium correspond to a transition from planar (160 Å pore diameter) to cylindrical (24 Å pore diameter) to slit geometries.

     

    The co-authors on the papers
    C. Andreani, C. Pantalei, R. Senesi

    References

 

Notes to editors. Other inelastic neutron scattering studies at high wavevector performed on liquid and solid 3He and 4He, and on 3He–4He mixtures via Deep Inelastic Neutron Scattering (DINS).

Contact details:
For more information, please contact Dr. Claudia Pantalei, tel: +39 06 72594429, E-mail

Related Information
Dr. R. Senesi, Prof. C. Andreani
DINS

Tags: ,